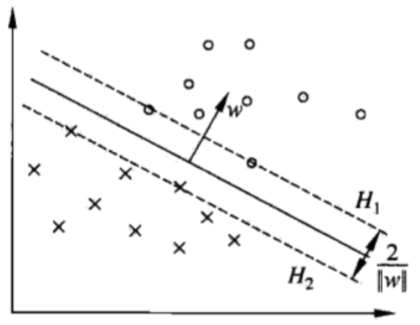
支持向量机SVM

支持向量机的学习策略是间隔最大化, 学习算法是求解凸二此规划的最优化算法.

• 线性可分支持向量机 ：
  • 硬间隔最大化 (hard margin maximization)
  • 硬间隔支持向量机
• 线性支持向量机 ：
  • 软间隔最大化 (soft margin maximization)
  • 软间隔支持向量机
• 非线性支持向量机 ：
  • 核函数 (kernel function)
  • 核方法

线性可分支持向量机

输入: 线性可分训练集 $T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$, 其中$x_i\in{\scr {X}}=R^n, y_i\in{\scr {Y}}=\{+1,-1\}$

函数间隔

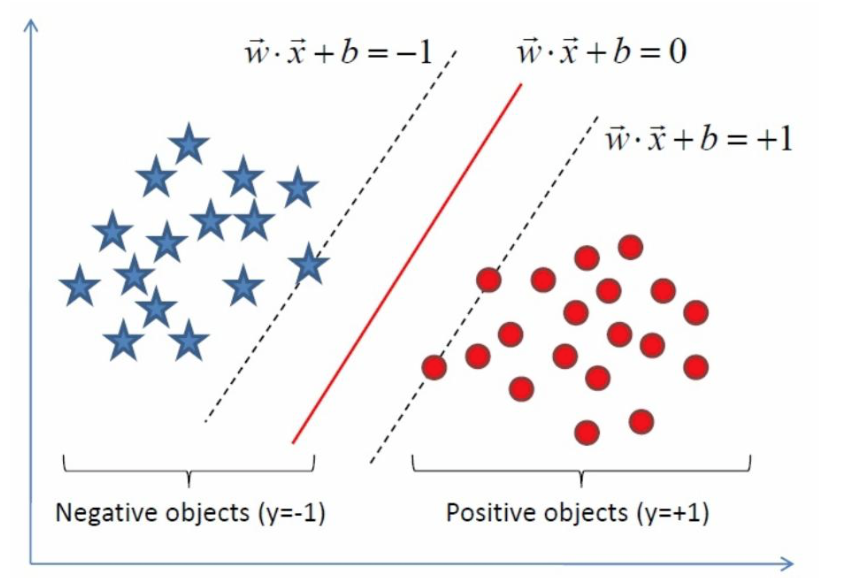
• 分离超平面: $w\cdot x+b=0$
• 一个点到分离超平面的距离为: $|w\cdot x+b|$
• 分类是否正确: $w\cdot x+b$ 的符号与 $y$ 的符号是否一致
• 分类的正确性及确信度 : $y(w\cdot x+b)$
• 超平面 $(w,b)$ 关于样本点 $(x_i,y_i)$ 的函数间隔:$\hat{\gamma_i}=y(w\cdot x_i+b)$
• 超平面 $(w,b)$ 关于训练数据集 $T$ 的函数间隔: $\hat{\gamma}= \min_{i=1,\cdots,N}\hat{\gamma_i}$

  几何间隔

• 超平面 $(w,b)$ 关于样本点 $(x_i,y_i)$ 的几何间隔:$\gamma_i=y(\frac{w}{\lVert w\Vert}\cdot x_i+\frac{b}{\lVert w\Vert})=\frac{\hat{\gamma_i}}{\lVert w\Vert}$
• 超平面 $(w,b)$ 关于训练数据集 $T$的几何间隔: ${\gamma}= \min_{i=1,\cdots,N}{\gamma_i}=\frac{\hat{\gamma}}{\lVert w\Vert}$

PS: 若 $w,b$ 成比例地改变(即超平面不变), 函数间隔也会按此比例改变, 几何间隔不变.

线性可分支持向量机学习算法

一. 间隔最大化

1.求几何间隔最大的分离超平面:

$\begin{matrix} \max_{w,b} & \gamma\\ s.t. & y(\frac{w}{\lVert w\Vert}\cdot x_i+\frac{b}{\lVert w\Vert})\geq\gamma \end{matrix}$

2.换成函数间隔 $\Longrightarrow$

$\begin{matrix} \max_{w,b} & \frac{\hat\gamma}{\lVert w\Vert}\\ s.t. & y(\frac{w}{\lVert w\Vert}\cdot x_i+\frac{b}{\lVert w\Vert})\geq\frac{\hat\gamma}{\lVert w\Vert}\\ \longrightarrow & y(w\cdot x_i+b)\geq\hat\gamma \end{matrix}$

3.函数间隔的取值不影响最优化问题的解, 因此取 $\hat\gamma=1$:

$\begin{matrix} \max_{w,b} & \frac{1}{\lVert w\Vert}\\ s.t. & y(w\cdot x_i+b)\geq1 \end{matrix}$

4.等价于 $\Longleftrightarrow$

$\begin{matrix} \min_{w,b} & \frac{1}{2}{\lVert w\Vert}^2\\ s.t. & y(w\cdot x_i+b)-1\geq0 \end{matrix}$

这就是最终要求解的凸二次规划问题, 求解最优解$w^\ast,b^\ast$

二. 对偶算法

5.对应的Lagrange函数

$L(w,b,\alpha)= \frac{1}{2}{\lVert w\Vert}^2-\sum_{i=1}^{N}\alpha_iy_i(w\cdot x_i+b)+\sum_{i=1}^{N}\alpha_i$

其中, 拉格朗日乘子向量为 $\alpha=(\alpha_1,\alpha_2,\cdots, \alpha_N)^T, \alpha_i\geq0,i=1,2,\cdots,N$

6.原问题(primal problem): $\min_{w,b}\max_\alpha L(w,b,\alpha)$

7.原问题的对偶问题(dual problem):

$\max_\alpha\min_{w,b} L(w,b,\alpha)$

• 先对$w,b$求偏导: $\nabla_w L(w,b,\alpha)=0, \nabla_b L(w,b,\alpha)=0$

  得到: $w=\sum_{i=1}^N\alpha_iy_ix_i,\\\sum_{i=1}^N\alpha_iy_i=0$

• 再求对$\alpha$的极大:

$\begin{matrix} \max_{\alpha} & -\frac{1}{2}\sum_{i=1} ^N\sum_{i=1} ^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^{N}\alpha_i\\ s.t. & \sum_{i=1}^N\alpha_iy_i=0 \\ & \alpha_i\geq0,i=1,2,\cdots,N \end{matrix}$

三. 最大分离超平面

8.存在$w^\ast,b^\ast,\alpha^\ast$, $\alpha^\ast$ 是对偶问题的最优解, 此时 $w^\ast,b^\ast$ 是原问题的最优解.

$w^\ast=\sum_{i=1}^N\alpha_i^\ast y_ix_i\\ b^\ast = y_i -\sum_{i=1}^N\alpha_i^\ast y_i(x_i\cdot x_j)$

9.最大分离超平面: $w^\ast\cdot x+b^\ast = 0$, 即:

$\sum_{i=1}^N\alpha_i^\ast y_i(x\cdot x_i)+b^\ast = 0$

10.分类决策函数:

$f(x)=sign(w^\ast x+b^\ast )=sign(\sum_{i=1}^N\alpha_i^\ast y_i(x\cdot x_i)+b^\ast)$

线性可分的支持向量

支持向量(support vector) :

训练数据集的样本点钟与分离超平面距离最近的样本点, 即满足:

$y_i(w\cdot x_i+b)-1=0$

• 对于$y_i=+1$, 支持向量在超平面: $H_1: w\cdot x+b=1$
• 对于$y_i=-1$, 支持向量在超平面: $H_2: w\cdot x+b=-1$

间隔距离 :

• 间隔边界: $H_1和H_2$
• 间隔距离: $H_1和H_2$之间的距离, 等于: $margin = \frac{2}{\lVert w\Vert}$

线性不可分支持向量机