主题模型(一)--数学基础

五个步骤:

1. 一个函数：$\Gamma$ 函数
2. 四个分布：二项分布、多项分布、Beta分布、Dirichlet分布
3. 一个概念和一个理念：共轭先验和贝叶斯框架
4. 两个模型：pLSA、LDA
5. 一个采样：Gibbs采样

一个函数

$\Gamma$ 函数

$\Gamma(x)=\int_0^1 {t^{x-1}e^{-t}} \,{\rm d}t$

• 递归性质: $\Gamma(x+1)=x\Gamma(x)$
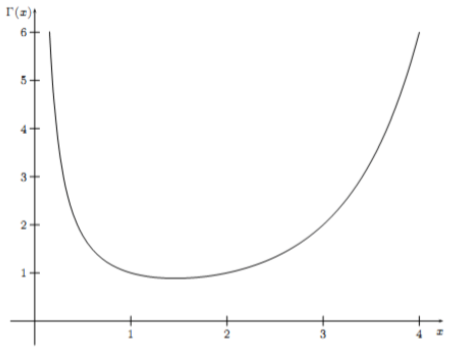
• $\Gamma$ 函数是阶乘在实数上的推广: $\Gamma(n)=(n-1)!$

四个分布

1. 二项分布

• 二项分布(Binominal), 是从伯努利分布(Bernouli)推进的. 简言之，只做一次实验，是伯努利分布，重复做了n次，是二项分布。
• 伯努利分布, 又称两点分布或0-1分布.是一个离散型的随机分布，其中的随机变量只有两类取值，非正即负{+，-}。
• 二项分布即重复n次的伯努利试验，记为$X\sim b(n,p)$ , 概率密度函数为： $f(k;n,p)=P(K=k)={n\choose k}p^k(1-p)^{n-k}$ 其中, ${n\choose k}=\frac{n!}{k!(n-k)!}=C_n^k$

2. 多项分布

• 多项分布(Multi-nominal)，是二项分布扩展到多维的情况。
• 多项分布是指单次试验中的随机变量的取值不再是0-1的，而是有多种离散值可能(1,2,3...,k). 比如投掷6个面的骰子实验，N次实验结果服从K=6的多项分布。其中: $\sum_{i=1}^kp_i=1, p_i>0$
• 多项分布的概率密度函数为: $f(x_1,x_2,\dots, x_k; n, p_1,p_2,\dots, p_k)=\frac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}$

3. Beta分布

Beta分布的概率密度: $f(x; \alpha, \beta)=\frac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta -1}, x\in (0,1)$ 其中, $B(\alpha, \beta)=\int_0^1 {x^{\alpha-1}(1-x)^{\beta-1}} \,{\rm d}x =\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$ 通过调节 $\alpha, \beta$, 可以得到Beta分布的各种形态. 可凸, 可凹, 可直, 可弯. 其中, 均匀分布也是特殊的Beta分布.

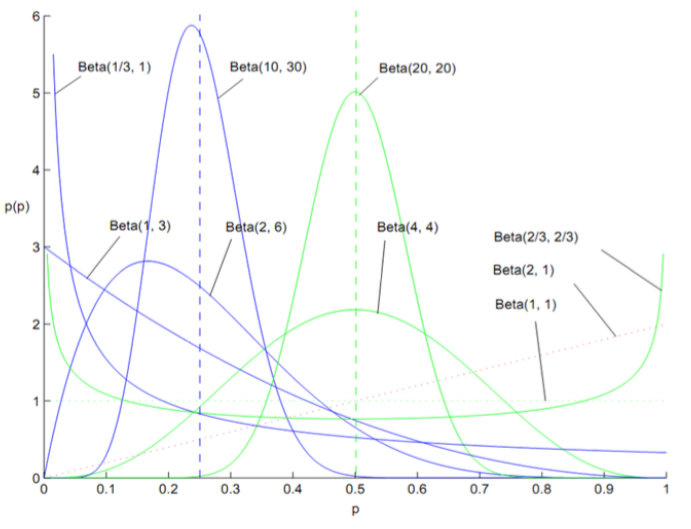
• Beta分布的期望: $E(x)=\int_0^1 {x\cdot f(x)} \,{\rm d}x=\frac{1}{B(\alpha, \beta)}\int_0^1 {x^{(\alpha+1)-1}(1-x)^{\beta-1}} \,{\rm d}x=\frac{B(\alpha+1, \beta)}{B(\alpha, \beta)}$ 即: $E(x)=\frac{\alpha}{\alpha + \beta}$

4. Dirichlet分布

• 维度 $K\geq2$ 的Dirichlet分布在参数 $\alpha_1, \dots, \alpha_K \geq 0$ 上, 基于欧几里得空间 (Euclidean Space) $R^{K-1}$ 里的勒贝格测度 (Lebesgue Measure)的概率密度函数:

  $f(x_1,\dots, x_K; \alpha_1,\dots, \alpha_K)=\frac{1}{B(\vec{\alpha} )}\prod_{i=1}^Kx_i^{\alpha_i-1}$

  其中, 概率密度函数定义在 $K-1$ 维的单纯形上, 其他区域的概率密度为0, $x_1,\dots, x_{K-1}>0,且x_1+\cdots+x_{K-1}<1, x_K=1-x_1-\cdots-x_{K-1}$

  归一化衡量 $B(\vec{\alpha})$ 是多项B函数 $B(\vec{\alpha}) =\frac{\prod_{i=1}^K\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^K\alpha_i)}, \qquad\vec{\alpha}=(\alpha_1,\dots, \alpha_K)$

• Dirichlet的另一种定义形式: $Dir(\vec{p}\mid\vec{\alpha})= \frac{1}{\Delta(\vec{\alpha})}\prod_{k=1}^Kp_k^{\alpha_k-1}$

  其中, $\Delta(\vec{\alpha})$ 称为Dirichlet分布的归一化系数: $\Delta(\vec{\alpha}) =\int_0^1 {\prod_{k=1}^Kp_k^{\alpha_k-1}} \,{\rm d}x =\frac{\prod_{i=1}^K\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^K\alpha_i)}$

• 特别的, 当参数 $\alpha_1=\dots=\alpha_K := \alpha$ 时, 称为 对称Dirichlet分布: $Dir(\vec{p}\mid\alpha,K)=\frac{1}{\Delta_K(\alpha)}\prod_{k=1}^Kp_k^{\alpha-1}, \quad\Delta_K(\alpha)=\frac{\Gamma^K(\alpha)}{\Gamma(K\cdot\alpha)}$

  • 当 $\alpha=1$, 退化为均匀分布
  • 当 $\alpha>1, p_1=p_2=\cdots=p_K$ 的概率增大

  • 当 $\alpha<1, p_i=1, p_{非i}=0$ 的概率增大

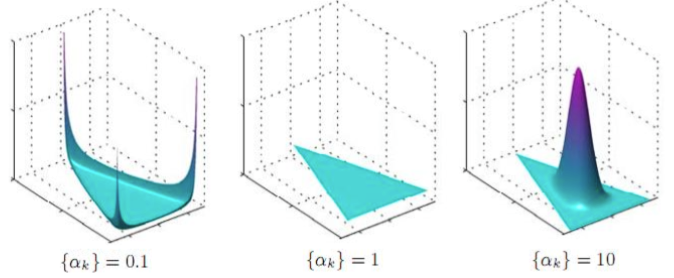
    取 $K=3$, 也就是有两个独立参数 $x_1,x_2$ ,分别对应图中的两个坐标轴,第三个参数始终满足$x_3=1-x_1-x_2且\alpha_1=\alpha_2=\alpha_3=\alpha$,图中反映的是 $\alpha$ 从0.3变化到2.0的概率对数值的变化情况。

    Dirichlet分布的概率密度函数取对数,绘制对称Dirichlet分布的图像

    从形式上可以看出, Dirichlet分布是Beta分布在高维度上的推广, 它和Beta分布一样也是百变的.

• Dirichlet分布的数学期望: 如果 $\vec{p}\sim Dir(\vec{t}\mid\vec{\alpha})$, 则:

  $E(\vec{p})=\left(\frac{\alpha_1}{\sum_{i=1}^K\alpha_i},\frac{\alpha_2}{\sum_{i=1}^K\alpha_i},\cdots, \frac{\alpha_K}{\sum_{i=1}^K\alpha_i} \right)$

一个概念和一个理念

共轭先验和贝叶斯框架

• 在贝叶斯概率理论中，如果后验概率 $P(\theta\mid x)$ 和先验概率 $P(\theta)$ 满足同样的分布律，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

• 根据贝叶斯公式可知： $P(\theta\mid x) = \frac{P(x\mid \theta)\cdot P(\theta)}{P(x)}\propto P(x\mid \theta)\cdot P(\theta)$

  注: 由于x为给定样本,P(x)有时被称为“证据”,仅仅是归一化因子, 如果不关心P(θ|x)的具体值, 只考察θ取何值时后验概率P(θ|x)最大,则可将分母省去。

• 贝叶斯派思考问题的模式: 先验分布 $P(\theta)$ + 样本信息 ${\scr{X}} \Longrightarrow$ 后验分布 $P(\theta \mid x)$

Beta-Binomial共轭

二项分布和Beta分布是共轭分布意味着，如果我们为二项分布的参数p选取的先验分布是Beta分布，那么以p为参数的二项分布用贝叶斯估计得到的后验分布仍然服从Beta分布。

对于非负实数 $\alpha,\beta$： $Beta(p\mid \alpha,\beta)+BinomCount(m_1,m_2)=Beta(p\mid \alpha+m_1,\beta+m_2)$

• $(m_1,m_2)是BinomCount(m_1,m_2)的计数$.
• $\alpha,\beta$ 先验性的给出了p分布,被称作 伪计数.

针对于这种观测到的数据符合二项分布，参数的先验分布和后验分布都是Beta分布的情况，就是Beta-Binomial共轭。换言之，Beta分布是二项式分布的共轭先验概率分布。

举例：

投掷一个非均匀硬币，可以使用参数为 $\theta$ 的伯努利模型，$m_1=x, m_2=1-x$ $\theta$ 为硬币为正面的概率，那么结果X的分布形式为：$P(x\mid \theta)=\theta^x\cdot(1-\theta)^{1-x}$

二项分布的共轭先验为beta分布，具有两个参数 $\alpha$ 和 $\beta$，称为超参数(hyper parameters)，且这两个参数决定了 $\theta$ 参数，其Beta分布形式为： $P(\theta\mid\alpha,\beta)=\frac{1}{B(\alpha,\beta)}\theta^{\alpha-1}\cdot(1-\theta)^{\beta-1}$

然后计算后验概率： $P(\theta\mid x) \propto P(x\mid \theta)\cdot P(\theta)\propto\left(\theta^x(1-\theta)^{1-x}\right)\left(\theta^{\alpha-1}(1-\theta)^{\beta-1}\right)=\theta^{x+\alpha-1}(1-\theta)^{1-x+\beta-1}$

因此, 后验概率是参数为 $(x+\alpha,1-x+\beta)$ 的另一个Beta分布, 即: 伯努利分布的共轭先验是Beta分布.

Dirichlet-Multinomial共轭

把 $\vec{\alpha}$ 从整数集延拓到实数集合, 从而得到更一般的表达式: $Dir(\vec{p}\mid\vec{\alpha})+MultCount(\vec{m})=Dir(\vec{p}\mid \vec{\alpha}+\vec{m})$

针对于这种观测到的数据符合多项分布，参数的先验分布和后验分布都是Dirichlet 分布的情况，就是Dirichlet-Multinomial 共轭。换言之，至此已经证明了Dirichlet分布的确就是多项式分布的共轭先验概率分布。

举例：

投掷一个骰子，可以使用参数为 $\vec{p}$ 的多项分布, $\vec{m}=\vec{x}$, $\vec{p}$ 为骰子各个面出现的概率, 那么结果X的分布形式为: $P(\vec{x}\mid \vec{p},N)=\frac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}={N\choose \vec{x}}\prod_{k=1}^K p_k^{x_k}$

多项分布的共轭先验为Dirichlet分布, 具K个超参数 $\vec{\alpha}$ ，且这K个参数决定了 K-1个 $\vec{p}$ 参数 $Dir(\vec{p}\mid\vec{\alpha})= \frac{1}{\Delta(\vec{\alpha})}\prod_{k=1}^Kp_k^{\alpha_k-1}$

然后计算后验概率： $P(\vec{p}\mid \vec{x}) \propto P(\vec{x}\mid \vec{p})\cdot P(\vec{p})\propto\prod_{k=1}^K p_k^{x_k}\prod_{k=1}^Kp_k^{\alpha_k-1}=\prod_{k=1}^Kp_k^{x_k+\alpha_k-1}$

因此, 后验概率是参数为 $\vec{\alpha}+\vec{x}$ 的另一个Dirichlet分布, 即: 多项分布的共轭先验是Dirichlet分布.

反馈与建议

• 微博：@Girl_AI

参考文献

• LDA数学八卦-rickjin(翻墙可看)
• 通俗理解LDA主题模型
• 七月算法机器学习在线班