贝叶斯网络

朴素贝叶斯

输入: 线性可分训练集 $T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$, 其中 $x_i\in{\scr {X}}=R^n, y_i\in{\scr {Y}}=\{c_1,\cdots,c_K\}$.
$X,Y$分别是定义在 ${\scr{X,Y}}$ 上的随机向量和随机变量.

$x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T, x_i^{(j)}=(a_{j1},a_{j2},\cdots,a_{jS_j}),$

条件独立性

朴素贝叶斯的基本假设是条件独立性: $P(X=x\mid Y=c_k)=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}\mid Y=c_k)\\ \qquad=\prod_{j=1}^n P(X^{(j)}=x^{(j)}\mid Y=c_k)$

• 优点: 这是较强的假设. 朴素贝叶斯法简单高效.
• 缺点: 牺牲了一定的分类准确率.

贝叶斯估计

• 先验概率分布的贝叶斯估计:

  $P_\lambda(Y=c_k)=\frac{\sum_{i=1}^N I(y_i=c_k)+\lambda}{N+K\lambda}$

• 条件概率分布的贝叶斯估计:

  $P_\lambda(X^{(j)}=a_{jl}\mid Y=c_k)=\frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k)+\lambda}{\sum_{i=1}^N I(y_i=c_k)+S_j\lambda}$

  其中, $\lambda\geq 0$ . 当 $\lambda=0$时, 是极大似然估计. 当 $\lambda=1$时, 为拉普拉斯平滑(Laplace smoothing)

Remark: 贝叶斯派思考问题的模式: 先验分布 $P(\theta)$ + 样本信息 ${\scr{X}} \Longrightarrow$ 后验分布 $P(\theta \mid x)$

贝叶斯定理

• 后验概率分布 $P(Y=c_k\mid X=x)=\frac{P(X=X\mid Y=c_k)P(Y=c_k)}{P(X)}\\ \qquad\qquad\qquad\qquad =\frac{P(X=x\mid Y=c_k)P(Y=c_k)}{\sum_kP(X=x\mid Y=c_k)P(Y=c_k)} \\ \qquad\qquad\qquad\stackrel{条件独立性}=\frac{P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}\mid Y=c_k)}{\sum_kP(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}\mid Y=c_k)}$
• 后验概率最大化 原理: 后验概率最大化, 等价于0-1损失函数的期望风险最小化 $y=arg\min_{c_k}\frac{P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}\mid Y=c_k)}{\sum_kP(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}\mid Y=c_k)}\\ =arg\min_{c_k}{P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}\mid Y=c_k)}$

Example

(来自北大<机器学习与自然语言处理>的PPT)

其中, 有可能概率为0, 需要去0化

贝叶斯网络

定义

$BN(G, \Theta)$: 贝叶斯网络(Bayesian Network)

$G$:有向无环图 (Directed Acyclic Graphical model, DAG)

$G$的结点:随机变量${X_1,X_2...X_n}$

$G$的边:结点间的有向依赖

$\Theta$:所有条件概率分布的参数集合

结点$X$的条件概率: $P(X|parent(X))$

每个结点所需参数的个数:

若结点的$parent$数目是$M$,结点和$parent$的可取值数目都是$K:K^M*(K-1)$

一个简单的贝叶斯网络

• $P(a,b,c)=P(c\mid a,b)P(a,b)=P(c\mid a,b)P(b\mid a)P(a)$!

全连接贝叶斯网络

• 每一对结点之间都有边连接 $P(x_1,x_2,\cdots,x_K)=P(x_K\mid x_1,\cdots,x_{K-1})\cdots P(x_2\mid x_1)P(x_1)$

  一个"正常"的贝叶斯网络

  
• 有些边缺失
• $x_1, x_2$独立
• $x_6, x_7$在$x_4$给定的条件下独立
• $P(x_1)P(x_2)P(x_3)P(x_4\mid x_1, x_2, x_3)P(x_5\mid x_1, x_3)P(x_6\mid x_4)P(x_7\mid x_4, x_5)$

条件独立判定

1. tail-to-tail

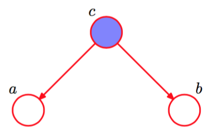
• 在$c$给定的条件下, $a,b$ 被阻断(blocked), 是独立的 $P(a,b\mid c)=P(a\mid c)P(b\mid c)$

2. head-to-tail

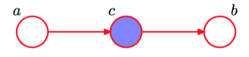
• 在$c$给定的条件下, $a,b$ 被阻断(blocked), 是独立的 $P(a,b\mid c)=P(a\mid c)P(b\mid c)$

3. head-to-head

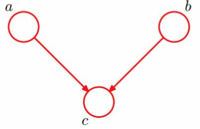
• 在$c$未知的条件下, $a,b$ 被阻断(blocked), 是独立的 $P(a,b)=P(a)P(b)$

有向分离

推广到结点集, 有向分离(D-separation): 对于任意的结点集A,B,C,考察所有通过A中任意结点到B中任意结点的路径,若要求A,B条件独立,则需要所有的路径都被阻断(blocked),即满足下列两个前提之一: 1) A和B的“head-to-tail型”和“tail-to-tail型”路径都通过C;
2) A和B的“head-to-head型”路径不通过C以及C的子孙;

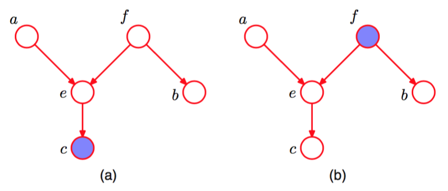
图(a), 在tail-to-tail中, f没有阻断; 在head-to-head中, e阻断, 然而它的子孙c没有阻断, 即e所在的结点集没有阻断; 因此, 结点a, b关于c不独立. 图(b), 在tail-to-tail中, f阻断; 因此, 结点a,b关于f 独立. 在head-to-head中, e和它的子孙c都阻断; 因此, 结点a,b关于e独立.

特殊的贝叶斯网络

1. 马尔科夫模型

• 结点形成一条链式网络,称作马尔科夫模型
• 由D-separation可知, 当$A_{i}$给定时, $A_{i+1}$与 $A_{1},A_{2},\cdots, A_{i}$条件独立; 即, $A_{i+1}$只与$A_{i}$有关,与$A_{1},\cdots,A_{i-1}$无关
• $P(A_{i+1}=a\mid A_{1}, A_{2},\cdots,A_{i})=P(A_{i+1}=a\mid A_{i} )$

2. 隐马尔科夫模型

Hidden Markov Model

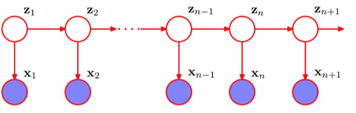
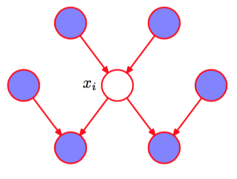
3. 马尔科夫毯

Markov Blanket : 一个结点的Markov Blanket是它的parents,children以及spouses(孩子的其他parent)

反馈与建议

• 微博：@Girl_AI

参考文献

• 统计学习方法
• Pattern Recognition and Machine Learning
• 七月算法机器学习在线班