主题模型(二)--pLSA&LDA

两个模型之一: pLSA模型

K个V 面的骰子

想象某个人要写 $M$ 篇文档，他需要确定每篇文档里每个位置上的词。假定他一共有 $K$ 个可选的主题，有 $V$ 个可选的词项，所以，他制作了 $K$ 个 $V$ 面的 “主题-词项” 骰子，每个骰子对应一个主题，骰子每一面对应要选择的词项。然后，每写一篇文档会再制作一颗 $K$ 面的 ”文档-主题“ 骰子；每写一个词，先扔该骰子选择主题；得到主题的结果后，使用和主题结果对应的那颗”主题-词项“骰子，扔该骰子选择要写的词。他不停的重复如上两个扔骰子步骤，最终完成了这篇文档。重复该方法 $M$ 次，则写完所有的文档。在这个过程中，我们并未关注词和词之间的出现顺序，所以 $pLSA$ 也是一种词袋方法.

pLSA的图

概率图

$D$ 代表文档, $Z$ 代表主题(隐含类别), $W$ 代表单词:

该模型假设一组共现(co-occurence)词项关联着一个隐含的主题类别 $z_k\in\{z_1,...,z_K\}$. 有如下三个相关的概率:

• $P(d_i)$ 表示词在文档 $d_i$ 中出现的概率;
• $P(z_k\mid d_i)$ 表示某个主题 $z_k$ 在给定文档 $d_i$ 下出现的概率;
• $P(w_j\mid z_k)$ 表示某词 $w_j$ 在给定主题 $z_k$ 下出现的概率;

pLSA的生成模型:

1. 按照概率 $P(d_i)$ 选择一篇文档 $d_i$
2. 按照概率 $P(z_k\mid d_i)$ 选择一个隐含的主题类别 $z_k$
3. 按照概率 $P(w_j\mid z_k)$ 生成一个词 $w_j$

即: $$\begin{align} P(d_i,w_j) &= P(d_i)P(w_j\mid d_i) \notag\\ &= P(d_i) \sum_{k=1}^K P(w_j, z_k\mid d_i)\notag\\&= P(d_i) \sum_{k=1}^K P(w_j\mid z_k)P(z_k\mid d_i) \notag\end{align}$$

其中, $\because$根据贝叶斯网络性质, $P(w_j,z_k,d_i)=P(w_j\mid z_k)P(z_k\mid d_i)P(d_i)\\$ $\therefore$ $P(w_j, z_k\mid d_i) = \frac{P(w_j,z_k,d_i)}{P(d_i)}=P(w_j\mid z_k)P(z_k\mid d_i)$

从矩阵的角度理解 $P(z_k\mid d_i)$ & $P(w_j\mid z_k)$

假设用 $\phi_k$ 表示词表 $\mathcal{V}$ 在主题 $z_k$ 上的一个多项分布，则 $\phi_k$ 可以表示成一个向量，每个元素 $\phi_{k,j}$ 表示词项 $w_j$ 出现在主题 $z_k$ 中的概率，即: $P(w_j\mid z_k) = \phi_{k,j}, \quad \sum_{w_j \in \mathcal{V}} \phi_{k,j} = 1$ 同样，假设用 $\theta_i$ 表示所有主题 $\mathcal{Z}$ 在文档 $d_i$ 上的一个多项分布，则 $\theta_i$ 可以表示成一个向量，每个元素 $\theta_{i,k}$ 表示主题 $z_k$ 出现在文档 $d_i$ 中的概率，即: $P(z_k\mid d_i) = \theta_{i,k}, \quad \sum_{z_k \in \mathcal{Z}} \theta_{i,k} = 1$ 最终我们要求解的参数是这两个矩阵： $$\begin{align} \Phi &= [\phi_1,\cdots,\phi_K]^T, \quad z_k \in \mathcal{Z} \notag\\ \Theta &= [\theta_i, \cdots, \theta_M]^T, \quad d_i \in \mathcal{D} \notag \end{align}$$

目标函数

由于词和词之间是互相独立的，于是可以得到整篇文档 $N$ 个词的分布: $P(\mathcal{W}\mid d_i) = \prod_{j=1}^N P(d_i, w_j)^{n(d_i,w_j)}$ 并且文档和文档也是互相独立的，于是我们可以得到整个语料库的词的分布 (整个语料库 $M$ 篇文档, 每篇文档 $N$ 个词)： $P(\mathcal{W}\mid\mathcal{D}) = \prod_{i=1}^M \prod_{j=1}^N P(d_i, w_j)^{n(d_i,w_j)}$ 其中, $n(d_i,w_j)$ 表示词项 $w_j$ 在文档 $d_i$ 中的词频，

样本分布的对数似然函数

$$\begin{align} \ell(\Phi, \Theta) &= \sum_{i=1}^N \sum_{j=1}^M n(d_i, w_j) \log P(d_i, w_j)\notag \\ &= \sum_{i=1}^N n(d_i) \left(\log P(d_i) + \sum_{j=1}^M {n(d_i,w_j) \over n(d_i)} \log\sum_{k=1}^K P(w_j|z_k)P(z_k|d_i)\right) \notag\\ &= \sum_{i=1}^N n(d_i) \left(\log P(d_i) + \sum_{j=1}^M {n(d_i,w_j) \over n(d_i)} \log\sum_{k=1}^K \phi_{k,j} \theta_{i,k} \right) \notag\end{align}$$

其中, $n(d_i)$ 表示文档 $d_i$ 中词的总数, 总有 $n(d_i) = \sum_{w_j \in \mathcal{V}} n(d_i, w_j)$

EM算法

我们需要最大化对数似然函数来求解参数，对于这种含有隐变量的最大似然估计，我们还是需要使用EM方法。

1. E-step: 假定参数已知，计算此时隐变量的后验概率。 $$\begin{align} P(z_k|d_i,w_j) &= {P(z_k, d_i, w_j) \over \sum_{l=1}^K P(z_l, d_i, w_j)} \notag\\ &= {P(w_j|d_i, z_k)P(z_k|d_i)P(d_i) \over \sum_{l=1}^K \left( P(w_j|d_i,z_l)P(z_l|d_i)P(d_i) \right)} \notag\\ &= {P(w_j|z_k)P(z_k|d_i) \over \sum_{l=1}^K P(w_j|z_l)P(z_l|d_i)} \notag\\ &= {\phi_{k,j} \theta_{i,k} \over \sum_{l=1}^K \phi_{l,j} \theta_{i,l} } \notag\end{align}$$

2. M-step：带入隐变量的后验概率，最大化样本分布的对数似然函数，求解相应的参数。

观察上面的对数似然函数 $\ell(\Phi, \Theta)$ ，由于 $P(d_i)∝n(d_i)$ 也就是文档长度可以单独从样本计算，可以去掉不影响最大化似然函数； 此外，根据E-step的计算结果，把 $\phi_{k,j} \theta_{i,k} = P(z_k|d_i,w_j) \sum_{l=1}^K \phi_{l,j} \theta_{i,l}$ 代入 $\ell(\Phi, \Theta)$，于是我们最大化下面这个函数即可： $\ell(\Phi, \Theta)= \sum_{i=1}^M \sum_{j=1}^N n(d_i, w_j) \sum_{k=1}^K \log P(z_k|d_i,w_j) \sum_{l=1}^K\phi_{l,j} \theta_{i,l}$ $\because Q(z^{(i)})= P(z_k|d_i,w_j) \\\therefore\ell(\Phi, \Theta)=下界函数B(\Phi, \Theta)=\sum_{i=1}^M \sum_{j=1}^N n(d_i, w_j) \sum_{k=1}^K P(z_k|d_i,w_j) \log\left[ \phi_{k,j} \theta_{i,k} \right]$

这是一个多元函数求极值问题，并且已知有如下约束条件： $\sum_{j=1}^N \phi_{k,j} = 1 \\ \sum_{k=1}^K \theta_{i,k} = 1$

一般处理这种带有约束条件的极值问题，我们常用的方法是拉格朗日乘数法，引入拉格朗日乘子把约束条件和多元函数结合在一起，转化为无条件极值问题。这里我们引入两个乘子 $\tau$ 和 $\rho$ ，可以写出拉格朗日函数，如下：

$\mathcal{H} = \mathcal{L}^c + \sum_{k=1}^K \tau_k \left(1- \sum_{j=1}^N \phi_{k,j}\right) + \sum_{i=1}^M \rho_i \left(1- \sum_{k=1}^K \theta_{i,k}\right)$

需要求解 $\phi_{k,j}$ 和 $\theta_{i,k}$ ，分别求偏导，取0，可得如下等式： $\sum_{i=1}^M n(d_i, w_j)P(z_k|d_i,w_j) - \tau_k \phi_{k,j}=0, \quad 1 \leq j \leq N, 1 \leq k \leq K \\ \sum_{j=1}^N n(d_i, w_j)P(z_k|d_i,w_j) - \rho_i \theta_{i, k}=0, \quad 1 \leq i \leq M, 1 \leq k \leq K$

消去拉格朗日乘子，最终可估计出参数： $$\begin{align} \phi_{k,j} &= {\sum_{i=1}^N n(d_i,w_j)P(z_k|d_i,w_j) \over \sum_{m=1}^M\sum_{i=1}^N n(d_i,w_m)P(z_k|d_i,w_m)} \notag\\ \theta_{i, k} &= {\sum_{j=1}^M n(d_i,w_j)P(z_k|d_i,w_j) \over n(d_i)} \notag\end{align}$$

两个模型之二: LDA模型

LDA的图

概率图

在原始的pLSA模型中，我们求解出两个参数：“主题-词项”矩阵 $\Phi$ 和“文档-主题”矩阵 $\Theta$ ，但是我们并未考虑参数的先验知识；而LDA的改进之处，是对这俩参数之上分别增加了先验分布，相应参数称作超参数(hyperparamter)。

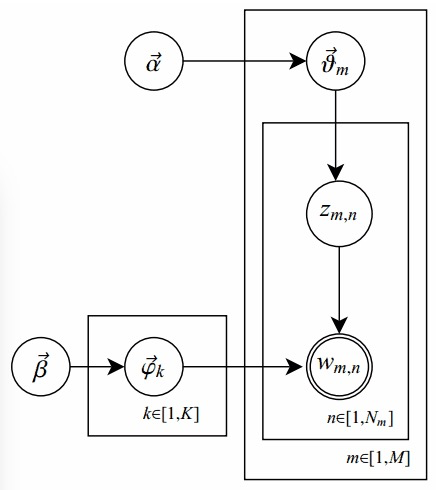
其中，单圆圈表示隐变量；双圆圈表示观察到的变量；把节点用方框(plate)圈起来，表示其中的节点有多种选择。所以这种表示方法也叫做plate notation.

对应到上图，只有 $w_{m,n}$ 是观察到的变量，其他都是隐变量或者参数，其中 $\vec{\alpha}$ 和 $\vec{\beta}$ 是超参数；方框中， $\Phi = \{\vec{\varphi}_k\}_{k=1}^K$ 表示有 $K$ 种“主题-词项”分布；$\Theta=\{\vec{\vartheta}_m\}_{m=1}^M$ 有 $M$ 种“文档-主题”分布，即对每篇文档都会产生一个 $\vec{\vartheta}_m$ 分布；每篇文档 $m$ 中有 $n$ 个词，每个词 $w_{m,n}$ 都有一个主题 $z_{m,n}$ ，该词实际是由 $\vec{\varphi}_{z_{m,n}}$ 产生。

LDA的生成模型

在LDA中，“文档-主题”向量 $\vec{\vartheta}_m$ 由超参数为 $\vec{\alpha}$ 的Dirichlet分布生成，“主题-词项”向量 $\vec{\varphi}_{z_{m,n}}$ 由超参数为$\vec{\beta}$ 的Dirichlet分布生成.

• 对所有的主题 $k\in[1,K]$ (生成 $\Phi$ : $K×V$ 矩阵)：
  • 生成“主题-词项”分布 $\vec{\varphi}_k\sim Dir(\vec{\beta})$ ( $V$ 维向量，对应词表 $\mathcal{V}$ 中的每个词项的概率)
• 对所有的文档 $m\in[1,M]$ (对应 $\Theta$ : $M×K$ 矩阵)：：
  • 生成当前文档 $m$ 相应的“文档-主题”分布 $\vec{\vartheta}_m\sim Dir(\vec{\alpha})$ ( $K$ 维向量，即第 $m$ 篇文档对应的每个主题的概率)
  • 生成当前文档 $m$ 的长度 $N_m \sim \mathrm{Poiss(\xi)}$
  • 对当前文档 $m$ 中的所有词 $n\in [1,N_m]$：
    • 生成当前位置的词的所属主题 $z_{m,n}\sim \mathrm{Mult}(\vec{\vartheta}_m)$
    • 根据之前生成的主题分布 $\Phi$ ，生成当前位置的词的相应词项 $w_{m,n} \sim \mathrm{Mult}(\vec{\varphi}_{z_{m,n}})$

目标函数

根据贝叶斯网络, 及所有已知信息和带超参数的隐变量，我们可以写出联合分布: $p(\vec{w}_m,\vec{z}_m,\vec{\vartheta}_m,\Phi|\vec{\alpha},\vec{\beta}) = \overbrace{ \underbrace{ \prod_{n=1}^{N_m} p(w_{m,n}|\vec{\varphi}_{z_{m,n}})p(z_{m,n}|\vec{\vartheta}_m) }_\text{word plate} \cdot p(\vec{\vartheta}_m|\vec{\alpha}) }^\text{document plate (1 document)} \cdot \underbrace{ p(\Phi|\vec{\beta}) }_\text{topic plate}$

通过对 $\vec{\vartheta}_m$ 和 $\Phi$ 积分以及 $z_{m,n}$ 求和，可以求得 $\vec{w}_{m}$ 的分布： $$\begin{align} p(\vec{w}_m|\vec{\alpha},\vec{\beta}) &= \int \int p(\vec{\vartheta}_m|\vec{\alpha}) \cdot p(\Phi|\vec{\beta}) \cdot \prod_{n=1}^{N_m} \sum_{z_{m,n}} p(w_{m,n}|\vec{\varphi}_{z_{m,n}}) p(z_{m,n}|\vec{\vartheta}_m) \mathrm{d}\Phi \mathrm{d}\vec{\vartheta}_m \notag\\ &= \int\int p(\vec{\vartheta}_m|\vec{\alpha}) \cdot p(\Phi|\vec{\beta}) \cdot \prod_{n=1}^{N_m} p(w_{m,n}|\vec{\vartheta}_m,\Phi) \mathrm{d}\Phi \mathrm{d}\vec{\vartheta}_m \notag\end{align}$$ 整个样本的分布： $p(\mathcal{W}\mid\vec{\alpha},\vec{\beta}) = \prod_{m=1}^M p(\vec{w}_m|\vec{\alpha},\vec{\beta})$

求联合分布 $p(\vec{w},\vec{z}\mid \vec{\alpha}, \vec{\beta})$

求出联合分布 $p(\vec{w},\vec{z})$ , 咱们便可以通过联合分布来计算在给定可观测变量 $w$ 下的隐变量 $z$ 的条件分布(后验分布) $p(\vec{z}\mid\vec{w})$ 来进行贝叶斯分析. $p(\vec{w},\vec{z}\mid \vec{\alpha}, \vec{\beta})=p(\vec{w}\mid\vec{z},\vec{\beta})\cdot p(\vec{z}\mid \vec{\alpha})$

• 第一部分 $p(\vec{w}\mid\vec{z},\vec{\beta})$ 表示的是根据确定的主题 $\vec{z}$ 和词分布的先验分布参数$\vec{\beta}$ 采样词的过程, 独立于 $\vec{\alpha}$
• 第二部分 $p(\vec{z}\mid \vec{\alpha})$ 根据主题分布的先验分布参数$\vec{\alpha}$ 采样主题的过程, 独立于 $\vec{\beta}$ 。

求第一个因子$p(\vec{w}\mid\vec{z},\vec{\beta})$

根据确定的主题 $\vec{z}$ 和从先验分布参数 $\vec{\beta}$ 采样得到的词分布 $\Phi$ 产生: $p(\vec{w}\mid\vec{z},\Phi) = \prod_{i=1}^W p(w_i\mid z_i) = \prod_{i=1}^W \varphi_{z_i,w_i}$ 由于样本中的 $\color{red}{W 个词服从参数为主题 z_i 的独立多项分布}$，这意味着，我们可以把上面的对词的乘积分解成对主题和对词项的两层乘积： $p(\vec{w}\mid\vec{z},\Phi) = \prod_{k=1}^K \prod_{\{i:z_i=k\}}p(w_i=t\mid z_i=k) = \prod_{k=1}^K \prod_{t=1}^V \varphi^{n^{(t)}_k}_{k,t} \tag 1$ 其中，$n_k^{(t)}$ 是词项 $t$ 在主题 $k$ 中出现的次数.

目标分布 $p(\vec{w}\mid\vec{z},\vec{\beta})$ 需要对 $\Phi$ 积分: $$\begin{align} p(\vec{w}\mid\vec{z},\vec{\beta}) &= \int p(\vec{w}\mid\vec{z},\Phi) p(\Phi\mid\vec{\beta}) \mathrm{d}\Phi \notag\\ &= \int \prod_{z=1}^K {1 \over \Delta(\vec{\beta})} \prod_{t=1}^V \varphi_{z,t}^{n_z^{(t)}+\beta_t-1} \mathrm{d} \vec{\varphi}_z \notag\\ &= \prod_{z=1}^K {\Delta(\vec{n}_z + \vec{\beta}) \over \Delta(\vec{\beta})}, \quad \vec{n}_z = \{n_z^{(t)}\}_{t=1}^V \notag\end{align}$$

求第二个因子$p(\vec{z}\mid\vec{\alpha})$

由于样本中的 $\color{red}{W 个词的主题 z_i服从文档d_i 的独立多项分布}$，这意味着，我们可以把上面的对词的乘积分解成对主题和对词项的两层乘积： $p(\vec{z}\mid\Theta) = \prod_{i=1}^W p(z_i\mid d_i) = \prod_{m=1}^M\prod_{k=1}^K p(z_i=k\mid d_i=m) = \prod_{m=1}^M\prod_{k=1}^K \theta_{m,k}^{n_m^{(k)}} \tag 2$ $d_i$ 是单词 $i$ 所属的文档，$n_m^{(k)}$ 是主题 $k$ 在文章 $m$ 中出现的次数

目标分布 $p(\vec{z}\mid\vec{\alpha})$ , 需要对 $\Theta$ 积分: $\begin{align} p(\vec{z}\mid\vec{\alpha}) &= \int p(\vec{z}\mid\Theta)p(\Theta\mid\vec{\alpha})\mathrm{d}\Theta\notag \\ &= \int \prod_{m=1}^M {1 \over \Delta(\vec{\alpha})} \prod_{k=1}^K \vartheta_{m,k}^{n_m^{(k)}+\alpha_k-1} \mathrm{d}\vec{\vartheta}_m \notag\\ &= \prod_{m=1}^M {\Delta(\vec{n}_m + \vec{\alpha}) \over \Delta(\vec{\alpha})}, \quad \vec{n}_m = \{n_m^{(k)}\}_{k=1}^K \notag\end{align}$

最终得到联合分布 $p(\vec{w},\vec{z}\mid \vec{\alpha}, \vec{\beta})$

$p(\vec{z},\vec{w}|\vec{\alpha},\vec{\beta}) = \prod_{z=1}^K {\Delta(\vec{n}_z+\vec{\beta}) \over \Delta(\vec{\beta})} \cdot \prod_{m=1}^M {\Delta(\vec{n}_m+\vec{\alpha}) \over \Delta(\vec{\alpha})}$

Gibbs 采样

所以，如果要完成Gibbs抽样，需要知道如下条件概率： $p(x_i\mid\vec{x}_{\neg{i}}) = {p(\vec{x}) \over p(\vec{x}_{\neg{i}})} = {p(\vec{x}) \over \int p(\vec{x})\mathrm{d}x_i}, \quad \vec{x} = \{x_i,\vec{x}_{\neg{i}}\}$ 如果模型包含隐变量 $\vec{z}$ ，通常需要知道后验概率分布 $p(\vec{z}\mid\vec{x})$ ，所以，包含隐变量的Gibbs抽样器公式如下： $p(z_i\mid\vec{z}_{\neg{i}}, \vec{x}) = {p(\vec{z},\vec{x}) \over p(\vec{z}_{\neg{i}},\vec{x})} = {p(\vec{z},\vec{x}) \over \int_Z p(\vec{z},\vec{x})\mathrm{d}z_i}$

LDA中的Gibbs采样

根据联合分布，求解下标为 $i=(m,n)$ 的词，即第 $m$ 篇文档中的第 $n$ 个词, 的全部的条件概率。

令 $\vec{w} = \{w_i=t, \vec{w}_{\neg{i}}\}, \quad\vec{z} = \{z_i=k, \vec{z}_{\neg{i}}\}$. 其中, $n_z^{(v)}$ 和 $n_{z,\neg i}^{(z)}$ 的关系式如下: $$n_z^{(v)} = \begin{cases} n_{z,\neg i}^{(v)}+1, & \text{if v=w_i=t and z=z_i} \\ n_{z,\neg i}^{(v)} , & \text{all other cases} \end{cases}\tag 3\\ $$ $$n_d^{(z)} = \begin{cases} n_{d,\neg i}^{(z)}+1, & \text{if z=z_i and d=d_i} \\ n_{d,\neg i}^{(z)} , & \text{all other cases} \end{cases}\tag 4\\ $$

LDA中的Gibbs采样: $$\begin{align} p(z_i=k\mid\vec{z}_{\neg{i}},\vec{w}) &= {p(\vec{w},\vec{z}) \over p(\vec{w},\vec{z}_{\neg{i}})} \notag\\ &= {p(\vec{w}\mid\vec{z}) \over p(\vec{w}_{\neg{i}}\mid\vec{z}_{\neg{i}}) p(w_i)} \cdot {p(\vec{z}) \over p(\vec{z}_{\neg{i}})} \notag\\ &\stackrel{忽略p(w_i)}\propto\prod_{z=1}^K {\Delta(\vec{n}_z+\vec{\beta}) \over \Delta(\vec{n}_{z,\neg{i}} +\vec{\beta})} \cdot \prod_{m=1}^M {\Delta(\vec{n}_m+\vec{\alpha}) \over \Delta(\vec{n}_{m,\neg{i}} +\vec{\alpha})} \notag\\ &\stackrel{式子(3)(4)}={\Delta(\vec{n}_z+\vec{\beta}) \over \Delta(\vec{n}_{z,\neg{i}} +\vec{\beta})} \cdot {\Delta(\vec{n}_m+\vec{\alpha}) \over \Delta(\vec{n}_{m,\neg{i}} +\vec{\alpha})} \notag\\ &\stackrel{式子(3)(4)}= {\Gamma(n_k^{(t)}+\beta_t)\Gamma(\sum_{t=1}^V (n_{k,\neg{i}}^{(t)}+\beta_t)) \over \Gamma(n_{k,\neg{i}}^{(t)}+\beta_t)\Gamma(\sum_{t=1}^V (n_k^{(t)}+\beta_t))} \cdot {\Gamma(n_m^{(k)}+\alpha_k)\Gamma(\sum_{k=1}^K (n_{m,\neg{i}}^{(k)}+\alpha_k)) \over \Gamma(n_{m,\neg{i}}^{(k)}+\alpha_k)\Gamma(\sum_{k=1}^K (n_m^{(k)}+\alpha_k))} \notag\\ &\stackrel{ \Gamma(x + 1) = x \Gamma(x)}= {n_{k,\neg{i}}^{(t)} +\beta_t \over \sum_{t=1}^V (n_{k,\neg{i}}^{(t)} +\beta_t)} \cdot {n_{m,\neg{i}}^{(k)} +\alpha_k \over \sum_{k=1}^K (n_{m, \neg{i}}^{(k)} +\alpha_k)} \notag\\ \end{align}$$

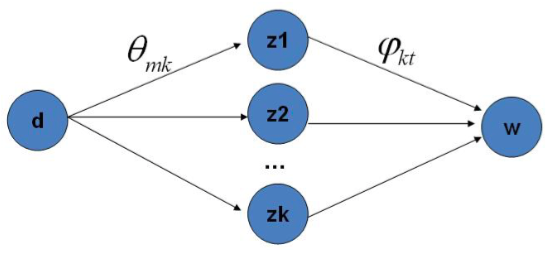
这个公式的右边其实就是 $p(topic\mid doc)\cdot p(word\mid topic)$, 这个概率其实是 $doc\rightarrow topic\rightarrow word$ 的路径概率. 由于 $topic$ 有 $K$ 个, 所以Gibbs Samppling 公式的物理意义就是在这 $K$ 条路径中进行采样.

求参数 $\Phi$ 和 $\Theta$

我们需要根据Markov链的状态 $z_i$ 获取多项分布的参数 $\Theta$ 和 $\Phi$ 。根据贝叶斯法则和Dirichlet先验，以及公式(1)和(2)： $$\begin{align} p(\vec{\vartheta}_m|\vec{z}_m,\vec{\alpha}) &= {1 \over Z_{\vartheta_m}} \prod_{n=1}^{N_m}p(z_{m,n}|\vec{\vartheta}_m) \cdot p(\vec{\vartheta}_m|\vec{\alpha}) = \mathrm{Dir}(\vec{\vartheta}_m|\vec{n}_m+\vec{\alpha}) \notag\\ p(\vec{\varphi}_k|\vec{z},\vec{w},\vec{\beta}) &= {1 \over Z_{\varphi_k}} \prod_{\{i:z_i=k\}}p(w_i|\vec{\varphi}_k) \cdot p(\vec{\varphi}_k|\vec{\beta}) = \mathrm{Dir}(\vec{\varphi}_k|\vec{n}_k+\vec{\beta}) \notag\end{align}$$ 求解Dirichlet分布的期望, 即可得: $$\begin{align} \varphi_{k,t} &= {n_k^{(t)}+\beta_t \over \sum_{t=1}^V n_k^{(t)} +\beta_t} \notag \\ \vartheta_{m,k} &= {n_m^{(k)}+\alpha_k \over \sum_{k=1}^K n_m^{(k)} +\alpha_k} \notag \end{align}$$

LDA Gibbs采样流程

反馈与建议

• 微博：@Girl_AI

参考文献

• Thomas Hofmann, Unsupervised Learning by Probabilistic Latent Semantic Analysis, Machine Learning, 42, 177–196, 2001
• Gregor Heinrich, Parameter estimation for text analysis
• David M.Blei, Andrew Y.Ng, Michael I.Jordan, Latent Dirichlet Allocation
• Wang Yi. Distributed Gibbs Sampling of Latent Topic Models: The Gritty Details Technical report, 2005.
• LDA数学八卦-rickjin(翻墙可看)
• 主题模型之pLSA
• 主题模型之LDA
• 通俗理解LDA主题模型
• 七月算法机器学习在线班