EM算法
密度估计
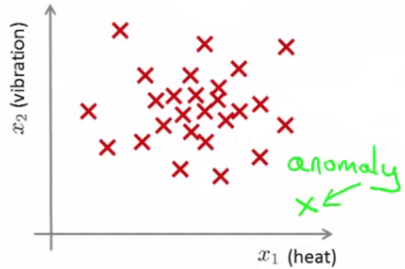
密度估计 (Density Estimation) 的一个应用是: 异常检测 (Anomaly Detection)
训练数据集为, 推出对应的概率分布模型 , 如果某个点偏离很多, 那么很有可能是异常点.
](1457526944690.png)
EM算法
只有输入没有对应的输出, 属于非监督学习问题: 训练数据集为个独立样本,希望从中找到该组数据的模型的参数, 是可观察值, 是未知的.
目标函数
对数似然函数:
最大化对数似然函数: z是隐随机变量, 不方便直接找到参数估计。
策略: 计算下界, 求该下界函数的最大值; 重复该过程, 直到收敛到局部最大值。
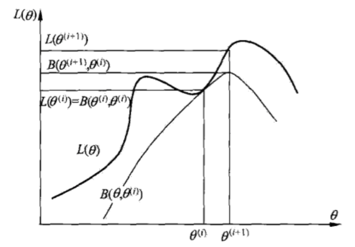
Jensen 不等式
- 定理: 是凸函数(e.g. ), X是随机变量, 则:
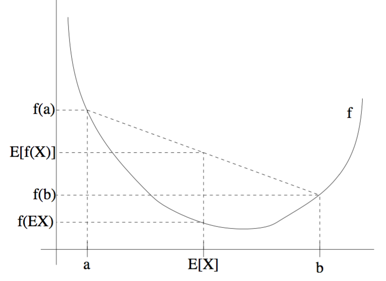
- 推论1: 若 (是严格的凸函数), 则 成立,
- 推论2: 若 (是严格的凹函数), 则
下界函数
即:
求
找尽量紧的下界函数, 即,
根据Jensen不等式的推论, 当且仅当:
即:
则:
EM算法整体框架 (非常重要!!@_@)
Repeat until convergence {
Step1. E-step (猜测 类标记 的值):
Step2. M-step (更新参数的估计):
Remark:
并列上升最优化( coordinate ascent optimization)
E-step: 求期望
M-step: 关于 最大化
EM在高斯混合模型中的应用
定义
- 一维高斯混合分布的例子。蓝色曲线给出了三个高斯分布(使用某个系数进行了缩放), 红色曲线表示它们的和:
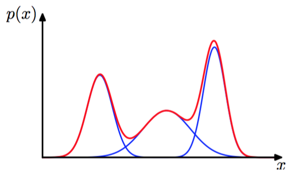
每个GMM由K个Gaussian分布组成:
- 每个Gaussian概率密度称为一个Component, 并且有自己的均值 和协方差 .
- 混合系数(mixing coefficient)为, 即每个 Component 被选中的概率, 满足:
加入隐变量
随机变量 是隐变量 ( latent / hidden / unobserved variables ) ,
之间的联合概率分布为: ,
假设: 从中随机选择得到; 而 根据 的取值, 由 个高斯分布中, 取第 个高斯分布中任意一点. 该模型称为高斯混合模型(GMM).
PS: GMM由2个高斯分布组成时,
目标函数
对数似然函数:
最大似然函数, 即求偏导,可得到参数的最大似然估计 (设问题集为):
EM在高斯混合模型中的算法过程
Repeat until convergence {
Step1. E-step (猜测 类标记 的值, 即计算此时隐变量的后验概率):
Step2. M-step (更新参数的估计):
}
EM & GDA
- 高斯判别分析 (Gaussian Discriminant Analysis, GDA)中, 类标记已知:
- EM中, 已知, 而类标记 未知:
M-step的推导
为求最大, 对各个参数求偏导:
- 对于 :
得到:
- 对于 :
考察M-step的目标函数, 对于, 删除常数项, 得到:
, 建立拉格朗日方程:
注: 这样求解的φi一定非负,所以,不用考虑 这个条件.
得到:
反馈与建议
- 微博:@Girl_AI